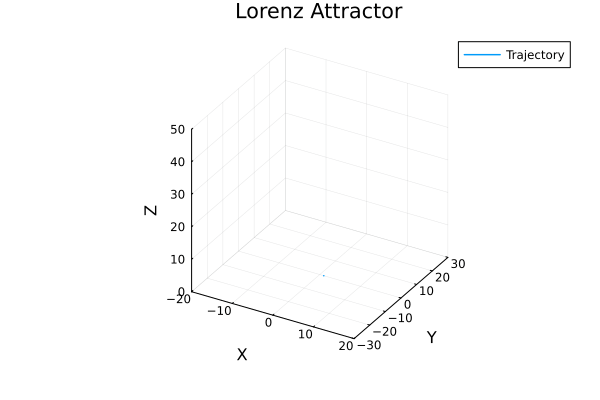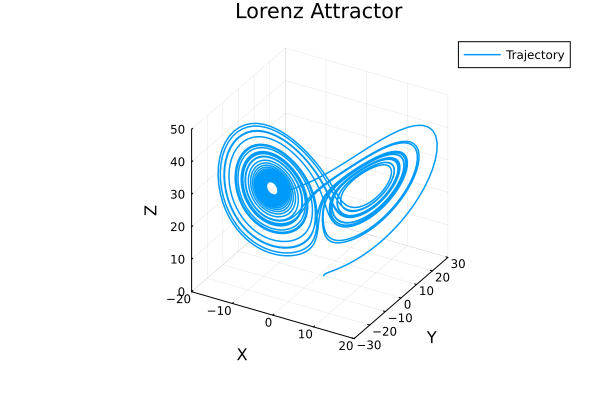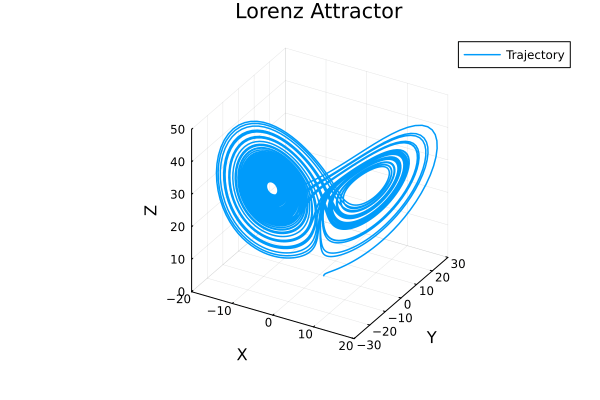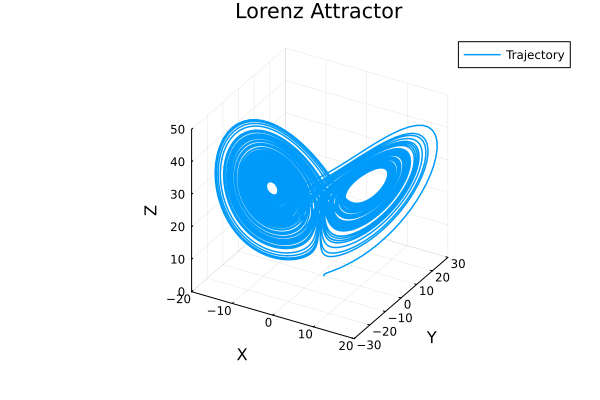
My research spans statistical physics, celestial mechanics, and dynamical systems. I study the statistical properties of complex and stochastic dynamical systems (e.g., epidemic and ecological models), and N-body problems in celestial mechanics—stability of planetary systems, symmetry breaking, and phase-transition-like phenomena. I’m also interested in connections between statistical physics and computer/data science.
Selected papers and preprints. Full list upon request.
We investigate why tensor networks—originally for quantum many-body systems—can model classical stochastic dynamics. By clarifying the underlying principles beyond 1D cases, we connect quantum and classical formalisms through operator/spectral viewpoints.
Stochastic generators expose deep links between spectra and macroscopic behaviors. I study how eigenvalue distributions relate to universality classes in nonequilibrium systems. Currently, I found spectral topology can affect dynamics and phase transitions in turbulence.
Central configurations yield self-similar N-body motions (homothetic expansion/contraction or rigid rotation). I explore analogies to symmetry breaking in statistical physics and map phase-diagram-like structures for symmetric 5-body configurations.
